CHAPTER FOUR
Resolution in CLS
The way into the calculus of Circles Letters and Subscripts (CLS), for the Resolution Method, is given us by Lemma 2.11. This says, a CLS expression E is mark-equivalent iff there exists a set of substitutions θ1, θ2... θn such that
Eθ1 Eθ2 ... Eθn = O,
where = denotes CL-equivalence (not mere CLS-equivalence). But if the expression on the left is equivalent to the mark, then, thanks to the argument of Chapter 3, we know that the mark can be derived from E by means of the resolution method.
We note that there is no obstacle to getting our expression E into clausal form, even though it contains atoms, involving subscripts, rather than simple letters. Essentially, the atoms that are distinct (including anywhere in their subscripts) can be treated just as if they were distinct letters, and the same procedure applied to E as worked for CL-expressions.
Therefore, there will be no loss of generality in assuming that E is in clausal form, although this will be mainly a matter of convenience in what follows. We note that a clause, transformed by a substitution, is either a) still a clause or b) void-equivalent. The latter case occurs when two atoms in the clause, one circled, the other not, are unified or made one by the substitution. Then the clause contains within its outer circle an expression of the form x(x), equivalent to the mark, which voids the clause. Consequently, if E is in clausal form, then so will be the expression occurring in Lemma 2.11. This leads us to a new version of the lemma:
Lemma 4.1
Suppose that a CLS expression E consists of a product of clauses
F G ... K .
A necessary and sufficient condition for E to be mark-equivalent is that there exists a set of substitutions θ1, θ2.. θm such that the collection of clauses
C1θ1 C2θ2 ... Cmθm
leads by a sequence of resolution-steps to the mark. Here each Ci is a member of the set {F, G ... K} and we do not insist that different Ci's stand for different members of the set. (In other words, the same clause F, G, or whatever, may be used more than once, with different substitutions.)
Proof
a) Necessity: the expression in Lemma 2.11 may be written
Fθ1 Gθ1 ... Kθ1 Fθ2 Gθ2 ... Kθ2 ... Fθn Gθn ... Kθn
which is of the form required for the present lemma (with m = n times the number of clauses in E). Note that in all likelihood very few of these clauses (Fθ1, etc.) will actually be required in the proof of mark-equivalence by resolution.
b) Sufficiency: we have
Eθ1 Eθ2 ... Eθm ≥ C1θ1 C2θ2 ... Cmθm ;
therefore, if the expression on the right-hand side of the equation dominates the mark, then so does the expression on the left. And if any expression dominates the mark, it is equivalent to the mark.
Finally, by Chapter 3, if any expression is CL-equivalent to the mark, than the mark can be derived from it by resolution◊
Definition 4.2 Reversible substitution, variant
A substitution θ is said to act reversibly on a factor F of an expression E if its denominator contains all the mutables occurring in F, and its numerator consists entirely of mutables that are 'new' to F - that is to say, that did not occur in F already, before its transformation by θ - and no two of which are the same. In other words, the effect of θ is that all the old mutables are thrown out and replaced by brand new ones.
Clearly, if φ is obtained from θ by turning upside-down each individual substitution (of letter for letter), then if we follow θ by φ the result is the identity substitution, so
F θ φ = F.
We may say that φ is the inverse of θ. (Equally, θ is the inverse of φ.)
If θ acts reversibly on F, we say that Fθ is a variant of F. Moreover, if F is a factor of a larger expression E, then the expression obtained from E by substituting a variant of F for F is said to be a variant of E.
Lemma 4.3
Variant expressions are CLS-equivalent. That is to say, if θ acts reversibly on F, then
F G ≅ Fθ G .
Proof
Suppose φ is the inverse of θ. Then
Fθ G ≅ Fθ Fθφ G = Fθ F G ≅ F G ◊
Remark 4.4
Since factors of expressions can be replaced by variant factors - without affecting CLS-equivalence - we may say, speaking loosely, that identity of mutables, occurring in different factors has no significance. Within a factor, identity of mutables does have significance, because all occurrences of the same mutable are affected equally by any substitution.
Lemma 4.5
An expression E is mark-equivalent iff there exists a resolution proof of
D1φ1 D2φ2 ... Dmφm = O
where each Di is a distinct variant of a clause of E, and each φi is a substitution. By 'distinct' we mean that each clause Di has its very own set of mutable letters, not shared with any of the others. (Immutables, on the other hand, may very well be shared between the different clauses.)
Proof
Suppose E is mark-equivalent. Then Lemma 4.1 applies, and we have a set of clauses Ci and substitutions θi such that the product of the Ciθi is CL-equivalent to the mark. Let the Ci be replaced by distinct variants Di related by reversible substitutions:
Di = Ciαi .
Each αi is invertible, with inverse βi, say. Then
Ci θi = Ci αi βi θi = Di φi,
where φi = βi θi. Conversely, if it is proved that
D1φ1 D2φ2 ... Dmφm = O
it follows that
Eθ1 Eθ2 ... Eθm = O,
where each θi is just αiφi. Therefore E is mark-equivalent ◊
Corollary 4.6
As their denominators (using that term to denote the set of mutables replaced by a substitution) are all distinct sets of mutables, the substitutions φi may be grouped into one 'big' substitution Φ and we may say that E is mark-equivalent iff there exists a resolution-proof of
D1Φ D2Φ ... DmΦ = O
Proof
For all i, Φ has the same effect as φi when it acts on Di ◊
The proof by resolution, mentioned in Corollary 4.6, must have a tree-structure. It must look something like this:
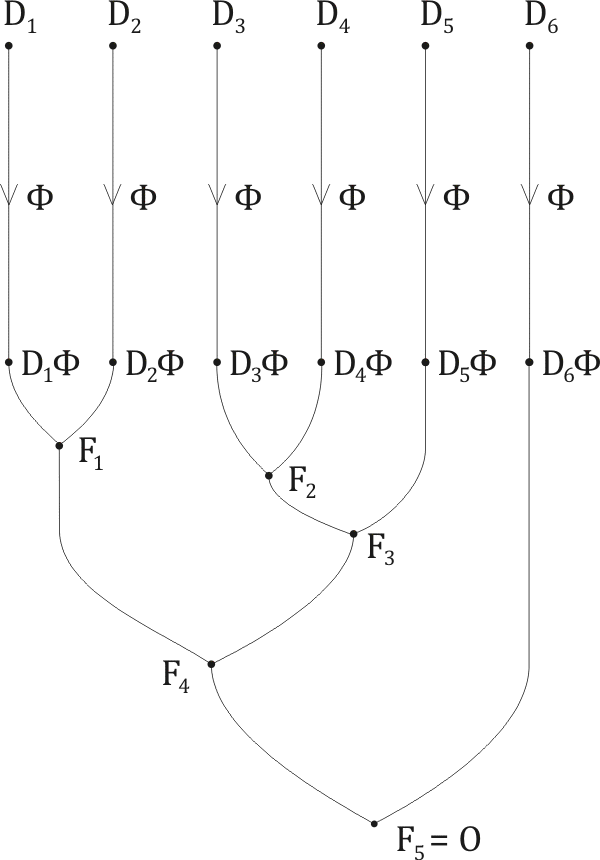
Here F1 (a clause) is the resolution-product of D1Φ and D2Φ; F2 is the resolution-product of D3Φ and D4Φ; F3 is the resolution-product of F2 and D5Φ; and so on, until we get to F5 which is the empty clause, in other words O. Of course, the actual derivation-tree is unlikely to have this exact form; but it will resemble this one in its general features.
Now for a crucial move. In the proof of Lemma 2.11 (back in Chapter 2) we made use of the 'Delay Principle' (Lemma 2.10), which said that when an expression is transformed by a sequence of CLS-allowed steps, we may assume that all the substitutions are done first, the CL-operations left until last. We now choose to put this idea into reverse. In the above diagram of the derivation-tree, we see that the substitutions (or rather, the one big substitution) is done first (i.e. at the top), then the resolution-steps (lower down). The new idea is to bring forward the resolution-steps as far as possible (bring them nearer to the top), while putting off the substitutions for as long as possible (moving them nearer to the bottom). There is a limit as to how far we can take this idea, for in the CLS-calculus the substitutions do after all serve an essential purpose: they transform certain atoms in the various clauses so that they become identical to one another and can be treated as though they were 'the same letter' for the purposes of CL-operations (in this case, resolution-steps). This enables the resolution-steps (requiring identical atoms to appear in two clauses) to be made. Without the substitutions, the steps would, in most cases, be impossible.
Referring to our diagram, we might ask: What is the minimum amount of substitution that is necessary to get say D1 and D2 to interact with each another - i.e. to link up (as clauses) by means of a resolution step? Evidently the substitution Φ suffices; which means that a certain atom in D1 and a certain atom in D2 are both transformed by Φ into one and the same atom (circled in one clause, not in the other), which can then be 'cancelled out' in the resolution step. But this amount of substitution may be more than is strictly necessary.
What is this 'amount of substitution'? Suppose one is trying to prove that a CLS-expression E is mark-equivalent. Then the mutability of the indices present in E is essentially a precious resource, analogous to water sitting at the top of a hill. A substitution can decrease, but never increase the total mutability present in an expression - and once an instance has become a ground instance, no further change is possible at all. All its potential is used up - like water that has flowed to the bottom of the hill and has reached 'ground level'. If we're thinking like a hydraulic engineer, we will want to eke out the potential of the water as far as possible - or, in the parallel case, eke out the mutability as far as possible.
As it turns out, a quite precise meaning can be given to the phrase 'minimum necessary amount of substitution', as we shall see in the next subsection.
Unification
This is the situation: we are given an atom a in one clause, and a circled atom (b) in a second clause. This is the first question: Is it possible to unify a and b, that is, make them identical or make them one by means of a substitution θ, working on the indices of a and b? This is the second question: Supposing there is such a θ, how may we ensure that is as minimal as possible?
Suppose we call any θ which 'makes one' a and b, a unifier of a and b. A unifier θ0 is said to be a minimal or most general unifier (or m.g.u. for short) if it has the following property. Let φ be any unifier of a and b; then there exists a substitution φ' such that φ may be expressed as a combination of substitutions
φ = θ0 • φ'
(meaning, do θ0 first, then φ').
Lemma 4.7 Unification Lemma
If two atoms a and b have a unifier, then they have an m.g.u.
Proof
The proof is a little intricate, although not really difficult, so we have banished it to a separate page. Here we merely offer some remarks.
If two atoms a and b are to have any hope at all of being unified, they must have the same 'head' (the part that is represented by a capital letter, e.g. P). For the head is not changed by any substitution. Secondly, if any index (at any level) of one atom is mixed, with an immutable head, and a partly mutable subscriptum, then the corresponding index in the second atom must be either i) mutable or ii) immutable or mixed but with the same head. If the two atoms have mixed indices with different heads, in corresponding places, the case is hopeless: no unification is possible. So long as there is either mutability or sameness-of-head, there is hope.
The key to the proof is an algorithm, which takes as input two atoms, and gives a 'verdict' (i.e. SUCCEED or FAIL) on the question, whether the two atoms are capable of unification. In the first case (success) the algorithm produces as a side-effect a substitution θ which can be shown to satisfy the properties required of an m.g.u.
Example 4.8
(taken from J.A.Robinson Logic: Form and Function, page 195). Let us take for our two atoms
Pxfgyfx , Phyzfzfhuv .
Can they be unified? Well, both atoms have the same head (letter P), which is a good start. And each P has three indices in its subscriptum, which is as it should be. Let's look at the first index, which is just mutable x in one case, and mixed index
hyz
in the other. This is OK: we can deal with it. We just transform both atoms by the substitution
{ hyz / x }
giving us
Phyzfgyfhyz , Phyzfzfhuv .
That wasn't too bad, was it? Now the first indices are unified, and it's time to go on to the second ones. These are
fgy, fz ;
both mixed, but with the same head: good! To unify them, we just need to unify z and gy, which means following up the first substitution with a second, namely
{ gy / z } ,
giving us
Phygyfgyfhygy , Phygyfgyfhuv .
On to the third indices
fhygy , fhuv ;
These can be sorted out using the substitution
{ y/u , gy / v },
leading to
Phygyfgyfhygy , Phygyfgyfhygy .
The atoms have indeed been made one. The unifying substitution is
{ hygy / x , gy / z , y/u , gy / v };
and this is in fact an m.g.u., although to see this you must refer to the proof of the Unification Lemma.
With unification under our belt, we can get back to work on our derivation-tree. Our aim is to convert the proof from 'substitute first, then resolve' to 'only substitute as much as you need to allow resolution to happen'. But the underlying structure of the proof (which clauses resolve, in what order) will stay the same. The first question to be answered, then, is How much substitution do we need to do on D1 and D2 to make the two clauses resolvable? (Note: we say that two clauses are resolvable if the very same atom appears in both clauses, circled in one and uncircled in the other.)
Well, we know that Φ will do the trick: D1Φ and D2Φ are resolvable because the existing derivation-tree says so. Therefore there is an atom in D1 and an atom in D2 which are unified by Φ. By the Unification Lemma, there is an m.g.u. ψ1 which unifies those same two atoms; and there exists a substitution Φ1 such that
Φ = ψ1•Φ1 .
On the face of it, ψ1 is a private matter for the two clauses D1 and D2 and has nothing to do with the other clauses. Certainly, it only acts on the mutables that occur in those two clauses. But knowing as we do that the mutables in all the other clauses Di are completely distinct, we may extend ψ1 to a substitution that acts on the whole expression D1 D2 ... Dm in a very straightforward way: it just does nothing at all to all those other mutables (the ones that don't occur in D1 or D2). Similar remarks apply to Φ1: on the one hand its scope is 'global' in the sense that it acts on the whole expression (the product of all the Di); on the other hand, it differs from Φ only in its action on the mutables of D1 and D2.
Now, the resolution-product of D1Φ and D2Φ is F1, a fact which we may represent in the following way:
F1 = Res[D1Φ,D2Φ].
Suppose we let
G1 = Res[D1ψ1,D2ψ1] ;
then
G1Φ1 = Res[D1ψ1,D2ψ1]Φ1 = Res[D1ψ1Φ1,D2ψ1Φ1] = Res[D1Φ,D2Φ] = F1 .
We have here made use of the following easy lemma:
Lemma 4.9
Let θ be any substitution. If clauses L and M resolve to N, then Lθ and Mθ resolve to Nθ
Proof
Since L and M are resolvable, there must be an atom a such that a occurs in L, and (a) occurs in M (or the other way round). But then aθ occurs in Lθ, and (a)θ, which is the same as (aθ), in Mθ. Therefore Lθ and Mθ are resolvable, and it is clear that their resolution-product is the same as Nθ ◊
We have performed a useful first step in the reform of our derivation-tree, which is worthy of being recorded in a new diagram (we include the old one on the left).
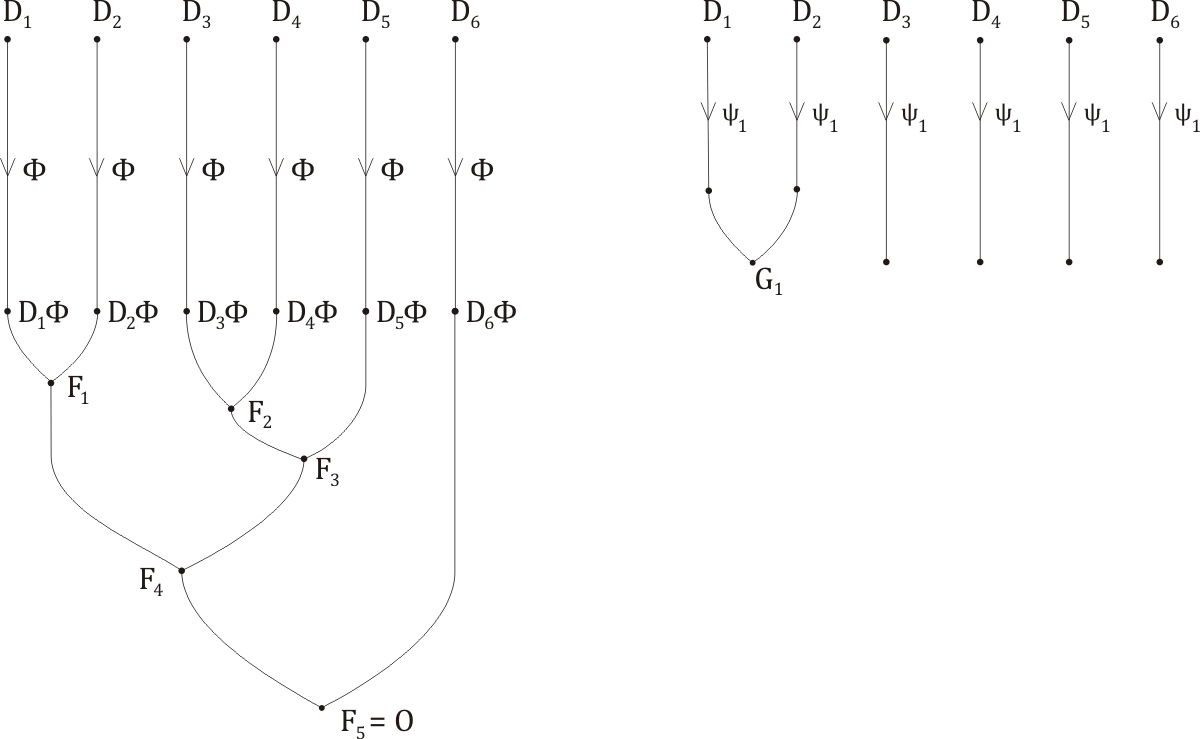
The next question is, How do we get D3ψ1 and D4ψ1 to resolve together? From the above, we know that they are made resolvable by the substitution Φ1; because
D3ψ1Φ1 = D3Φ, D4ψ1Φ1 = D4Φ .
But Φ1 is very unlikely to be the most general unifier of the corresponding atoms. However, there must exist an m.g.u., let's call it ψ2; then Φ1 can be decomposed as
Φ1 = ψ2•Φ2 ;
and G2, the resolution-product of D3ψ2 and D4ψ2, is related to F2 by
F2 = G2Φ2 .
Well, that was pretty easy. The next step is only slightly different. How do we get G2 to interact with D5ψ1ψ2? We know that F2 resolves with D5Φ. But F2 is the same as G2 Φ2, while D5Φ is the same as D5ψ1ψ2Φ2.
Thus Φ2 is a unifier for G2 and D5ψ1ψ2; which allows us to seek out an m.g.u. ψ3, and to decompose Φ2 as
Φ2 = ψ3•Φ3,
and so on...
... until eventually we come to G5, related to F5 by the equation
F5 = G5Φ5 .
But F5 is none other than the mark; so the clause G5 is turned into the mark (or 'the empty clause') by the action of a substitution (namely, Φ5). But mere substitution (i.e. not a CL-operation) cannot make any of the atoms, or circled atoms, within G5 go away or vanish. Therefore, G5 itself must be devoid of atoms: G5 is already the mark. Time for the full diagram:
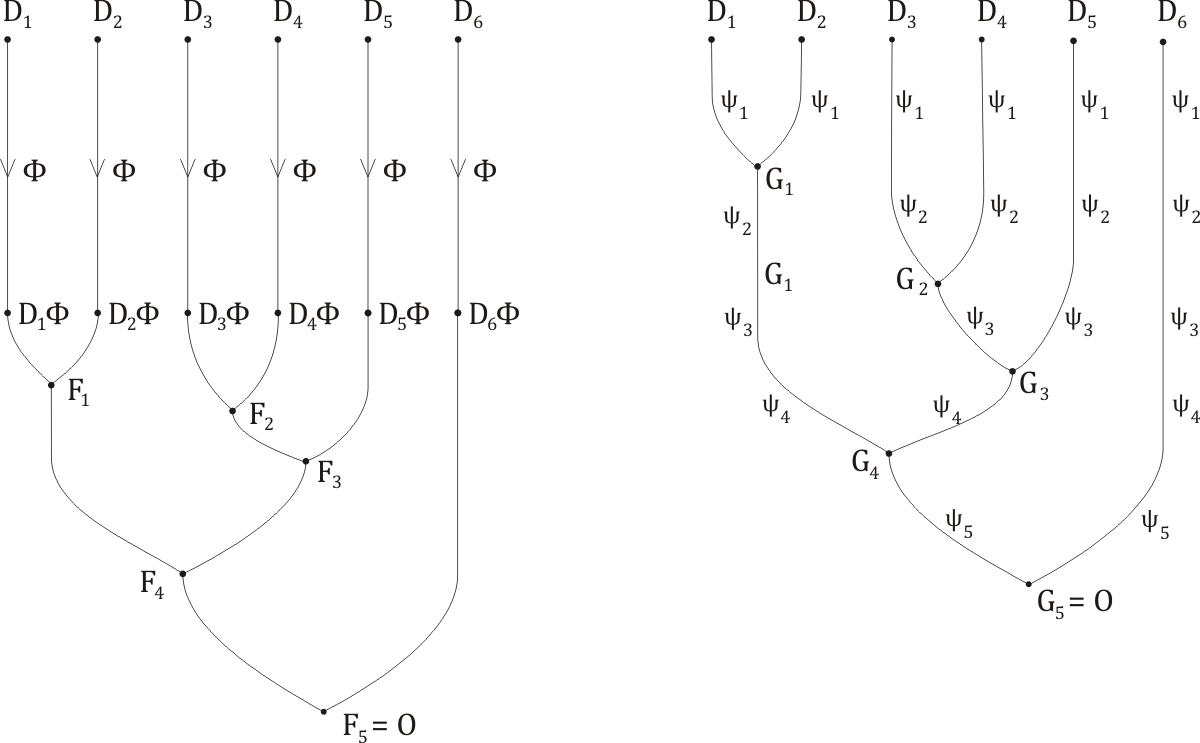
Let us take stock. We have effectively reproduced our original proof by resolution, but using the minimum possible amount of substitution. The method by which we have obtained the more elegant proof is really quite similar to the method of obtaining a minimal, or most general unifier (given in the page devoted to the Unification Lemma) - it is as it were unification writ large. Φ5 represents that part of the original global substitution, Φ, that turns out to be superfluous. However, economy or miserliness is not really our motivation! Far more important, as we shall see in a moment, the notion of the economical derivation-tree gives us a new and really quite revolutionary criterion for a CLS-expression to be mark-equivalent.
Suppose we have a hunch that an expression E is mark-equivalent. But we're not satisfied with our hunch, we want proof! Suppose we have no insight into why E is mark-equivalent, and that what we'd really like - to save us the trouble - is a method of seeking out a proof that a machine could use: an algorithm, in other words. We start by getting E into clausal form, then we replace clauses by variants, if necessary, so that each clause has its very own set of mutables. Each clause will be reusable in the procedure that is to follow, as many times as we like; but each time we use a clause to 'mate' with a second clause we replace the offspring (i.e. the resolution-product) by a variant which uses completely new mutables. In this way we make sure that the 'breeding stock' of clauses always satisfies the condition of 'no cross-over'; in other words, no sharing of mutables between different clauses.
Kindred Clauses
Let us say that two clauses are 'kindred' if they are capable of being made resolvable by the application of a substitution.
So if the two clauses are F, G, there is a θ such that Fθ and Gθ are resolvable. It will be recalled that 'resolvable' means that there is an atom which appears uncircled in one of Fθ and Gθ, circled in the other. Note that F and G may be kindred in more than one way: various substitutions may bring about unifications of different atom pairs. Note further that F and G may be variants of the same clause. In another way of speaking, G may be the same as F, only with different mutables. Neither F nor G may contain the exact same atom twice: the idea is that applying a substitution θ which acts differently on the letters of F and those of G, atoms which were different before may be made the same. (This will be made clearer by the examples.)
Example 4.10
Consider the two clauses:
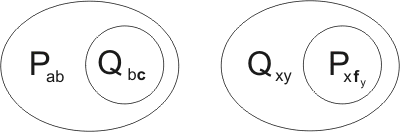
They are kindred in two ways. Firstly, Qxy may be unified with Qbc, by the substitution {b/x, c/y}. Under the action of this substitution, the clauses become
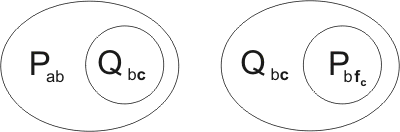
and their resolution-product is
Secondly, Pab is unified with Pxfy by {x/a, fy/c}; the clauses become
with resolution-product
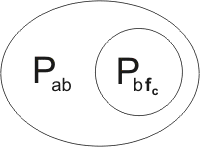
Finally, before adding the resolution-products to the breeding stock, we need to subject them to reversible substitutions, so that their mutables are distinct from any already present in the stock. So they might become, for example,
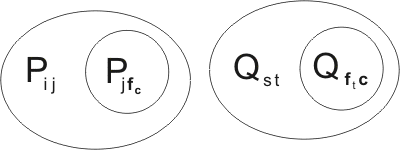
Note that the letters c and f, representing immutables, are unaffected by any substitutions. The same immutable may well appear in many different clauses.
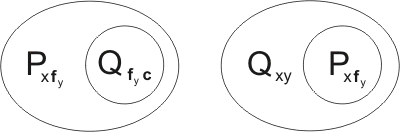
Example 4.11: Clause kindred with itself (Parthenogenesis)
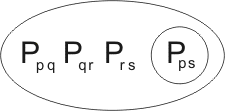
Consider the clause
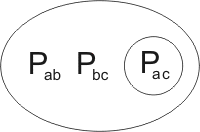
If we write beside it a variant of the same clause
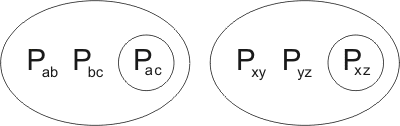
we see that the clause is kindred with itself. In fact it is kindred with itself in two ways: firstly, Pab may be united with Pxz by the substitution {x/a,z/b}:
leading to the resolution-product
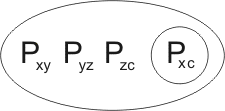
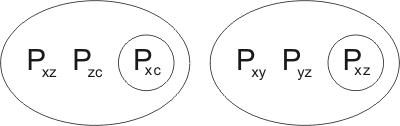
Secondly, Pbc may be united with Pxz, by {x/b,z/c}:
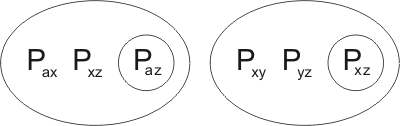
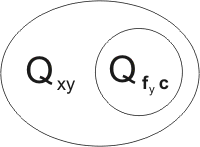
leading to
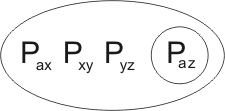
Closer inspection shows that this second resolution-product is in fact a variant of the first. Transforming the first by a reversible substitution we obtain the clause
to be added to the breeding stock.
If F and G are kindred, in n ways, let us call the n clauses which are the possible resolution-products, the 'progeny' of F and G. As usual, we must make sure that the n new clauses all employ different sets of 'new' mutables.
Given a set of clauses, the 'total progeny' of the set is defined in the first place as the union of the progenies of all kindred pairs of clauses taken from the set. Then we try each clause of the set with itself; it may be able to produce progeny by 'parthenogenesis', or mating with itself, as in the example just given. If so, these parthenogenetic offspring are added to the total progeny.
In summary, we have the following
Theorem 4.12: Resolution Theorem
Given an expression E, let E be converted into clausal form and let S0 be the set of clauses of E. Let S1 be the union of S0 with its total progeny; and in general let Sn+1 be the union of Sn with its total progeny. Then E is mark-equivalent if and only if there is an n such that Sn contains the empty clause (the mark).
Proof
By Corollary 4.6 we already have that E is mark-equivalent if and only if there exists a resolution-proof of
D1D2...DmΦ = 0
for some substitution Φ. Such a proof can be made 'parsimonious' (so far as substitution is concerned) by means of the procedure described above. In the parsimonious proof, the only substitutions employed are the 'most general unifiers' required to make two clauses or two-resolution products interact. But such interactions will all be 'discovered' by the breeding process: there is no way the breeding process could miss the actual parsimonious proof (although it might discover another one first!). Therefore there will be an Sn that contains the empty clause.
Conversely, suppose that O is contained in Sn for some n. Look at the 'family tree' of O i.e. the sequence of resolutions by which it was produced. Since each resolution-product is dominated by its parents, the family tree amounts to a proof that
D1D2...DmΦ = 0 ,
where the Di are the clauses that can be traced as the original ancestors of O, and Φ is the combination of the m.g.u's employed in the successive acts of resolution:
Φ = ψ1•ψ2•ψ2• ... •ψm-1.
Therefore E is mark-equivalent by Corollary 4.6 ◊