CHAPTER TEN (cont.)
Examples (Part Three)
Example 10.10
For our final, extended - not to say rambling - example we return to Group Theory, this time to the very beginnings of the theory - the axioms. It is normally said of the identity element e that both e•x and x•e must equal x for all elements x; similarly, it is said of the inverse x-1 of x that both x-1•x and x•x-1 must equal e. However, it is in fact sufficient to posit just the first of each of these pairs of statements, that is, that e is a 'left identity element' and that x-1 is a 'left inverse' of x. The other properties ('right identity element' and 'right inverse') follow from the first ones.
We would like to be able to show, then, that associativity, left-identity and left-inverse together imply right-identity and right-inverse. To start with we will focus our attention on just the first conclusion (right-identity). To make it a bit more formal, we would like to show that C follows from P1, P2, P3, P4, where the statements are defined as follows:
| P1 | ∀x ∀y ∀z ∀u ∀v ∀w (Rxyu∧Ryzv∧Ruzw) → Rxvw |
| P2 | ∀x ∀y ∀z ∀u ∀v ∀w (Rxyu∧Ryzv∧Rxvw) → Ruzw |
| P3 | ∀x Rexx |
| P4 | ∀x ∃y Ryxe |
| C | ∀x Rxex |
| ¬C | ∃x ¬Rxex |
Converting into CLS-expressions, our task is to show that the following expression is mark-equivalent:
You may like to try your hand at a direct approach to this problem, 'breeding' new expressions by resolution. I think you will soon find that the number of possible combinations is so great that progress toward the goal (the mark) is impossible. I decided to aim much lower, and see if I could adapt an existing (well-known) demonstration of the theorem to the CLS method. Even this turned out to be not without its own difficulties, as we shall see. Let's start by looking at the existing proof of the theorem that 'right-identity' follows from associativity, left-identity and left-inverse. It begins by establishing a lemma:
Lemma If h•h = h then h = e.
Proof Let g be the left-inverse of h, so g•h = e. Then
e = g•h = g•(h•h) = (g•h)•h = e•h = h ◊
Getting back to the main proof, let x be any element of G, and let y be its left-inverse; and let
h = x•y.
Then
h•h = (x•y)•(x•y) = ((x•y)•x)•y = (x•(y•x))•y = (x•e)•y = x•(e•y) = x•y = h.
Therefore, applying the lemma,
x•y = h = e,
and
x•e = x•(y•x) = (x•y)•x = e•x = x Q.E.D.
It will be noted that the proof requires no less than five applications of associativity (i.e. P1 and/or P2), as well as numerous applications of each of P3 and P4. In addition it makes much use of the notion of equality between group elements. But equality is not explicitly mentioned in our premises; at most implicitly in the use of the 3-place predicate Rxyz, which makes the claim that the combination of x and y (i.e. x•y) equals z.
To explain the problem with equality, let's think what is involved in translating the lemma into CLS-language. The immediate problem is that the conclusion of the lemma 'x = e' cannot be expressed in terms of the predicate Rxyz. Even to express the conclusion there is nothing for it but to introduce a new 2-place predicate Exy with the meaning 'x equals y'.
The core of the proof of the lemma is the fact that the triple product
ih•h•h
can be construed in 2 different ways
(ih•h)•h and ih•(h•h),
equivalent to
e•h and ih•h,
respectively, by P4 and by hypothesis (h•h = h). These combinations are equivalent, in turn, to h and e, respectively. But P1 and P2 won't quite yield us this result. Rather, they yield us the results
ih•h = h and e•h = e,
respectively. Of these, the second statement looks most promising; for, put together with P3, which implies e•h = h, it would seem to imply
Eeh,
i.e. that e and h are equal. However, 'seems to imply' is really not good enough - we are trying to do logic, after all! To do this thing properly, we need to define the properties of the relation (i.e. 2-place predicate) Exy. It looks like one of these properties ought to be:
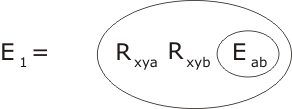
In words: if it is the case, for some x, y, a and b that the combination of x and y is a, and also that the same combination is b, then a equals b. That seems reasonable enough - or self-evident, as axioms are supposed to be - doesn't it? Besides, it gives us what we want, which is that h 'equals' e. We are now in a position to state and prove the lemma in the language of CLS. Just before that, I am going to slip in a little change. We don't want our hypothesis (translating h•h = h) to be Rhhh because, by the usual rules of interpretation, this would mean that Rhhh is true for all h. Rather, our hypothesis is that there is one particular h satisfying h•h = h; we express this by changing h into an immutable h. Here then is our lemma:
Lemma
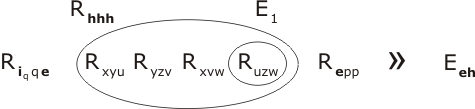
(For the meaning of the symbol » refer back to Chapter One.)
Proof
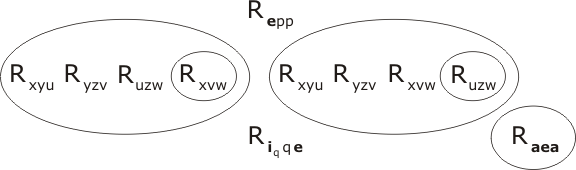
We first resolve P2 with Rhhh and two copies of P4. There is clearly a certain amount of choice as to which terms we attempt to unite (as R... and E.. are the only predicate-functions in town). Let us be guided by the 'natural language proof' of the lemma. Recall that this was based on the triple product ih•h•h; this tells us that ih will match up with the mutable x in P2, h with y and h with z. So the term Rhhh will match up with, indeed, unite with the term Ryzv within P2. Let's do that resolution first:
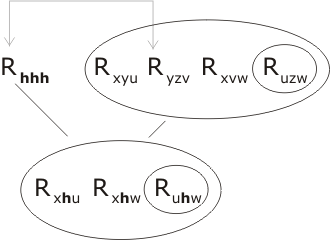
(the unifying substitution is simply {h/y, h/z, h/v}.) To unite the two remaining terms at level -1 with 2 copies of P4 the unifier is {h/q, h/r, ih/x, e/u, e/w } resulting in
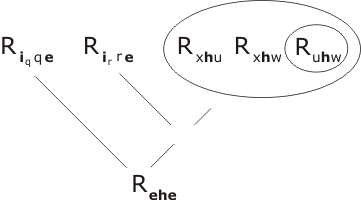
Note that we haven't bothered to draw in the intermediate resolution-product. In fact all three resolution-steps so far employed can be viewed as a single compound resolution step resulting from the union of the compound terms
Rxyu Ryzv Rxvw, Riqqe Rhhh Rirre
The unifier is the combination of the substitutions already given; and once the compound terms are united, the copy inside the circle can be uncopied (all three sub-terms at once), giving the result Rehe. We may use the following terminology to represent the whole process:
Res(P4, Rhhh, P4, P2) = Rehe .
Now that we have obtained the term Rehe we only need to resolve it with P3 and the equality premise E1 to complete the proof of the lemma:
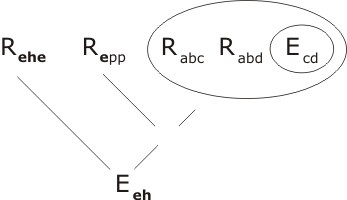
Q.E.D.
(We have obtained the statement Eeh. What we can actually do with it is another question, which we will address in due course.)
Actually, for our main proof we will need a lemma that is slightly stronger than the one just proved. The one we have only works for one particular h; ideally, we want one that works for any h that just happens to satisfy h•h = h. We obtain the slightly stronger lemma simply by omitting the premise Rhhh and seeing what we are given by the resolution process. This is the result:
Stronger Lemma
P4P2P3E1 » (Raba (Eeb)).
Proof
We resolve P2 with two copies of P4 by uniting the compound terms
Rxyu Rxvw, Rippe Riqqe .
The unifying substitution is determined as follows:
x = ip = iq ∴ q = p y = p u = e v = q = p w = e
Therefore Ruzw = Reze, and the resolution product is

Now resolve this expression with P3 and E1:
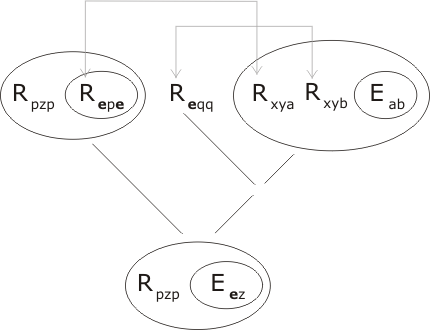
and the lemma is proved ◊
Corollary of the stronger lemma
The original lemma may be obtained from the stronger one by adding Rhhh into the premises and resolving◊
Now we've got the lemma out of the way, we return to the main proof, which starts
'Let h = x•ix'
How do we translate this? We can't just posit Rxixh, for this would be saying 'for all x the combination of x and ix is h'. No, h must be allowed to depend on x - to have x as a subscript. Our premise becomes
P5 = Rxixhx,
in words: "for all x there is an h such that h is equal to the combination of x and the inverse of x". (Indeed, this may be understood as a specialization of the more general axiom:
P0 = Rxyzxy.)
Step 1. At last we can make the first step of our proof. This consists of resolving P4, P5 and P3 with P1. We can do this as a compound resolution, as described above - a question of evaluating
Res(P4, P5, P3, P1).
The crucial thing is to unite the compound term consisting of the level -1 terms of P1 with the product P4P5P3, i.e.
Rxyu Ryzv Ruzw with Rippe Rqiqhq Rerr .
We calculate the unifying substitution as follows:
x = ip y = p = q z = iq = ip = r u = e v = hq = hp w = r = ip
This turns Rxvw (the consequence of P1) into
Riphpip,
thus
Res(P4, P5, P3, P1) = Riphpip.
Step 2. We calculate Res(P5, Riphpip, P5, P2). For this we must unite
Rxyu Ryzv Rxvw with Rpiphp Riqhqiq Rrirhr.
We calculate the unifying substitution as follows:
x = p = r y = ip = iq ∴ q = p z = hq = hp u = hp v = iq = ir = ip w = hr = hp
Therefore Ruzw (the conclusion) becomes
Rhphphp,
which is eminently satisfactory, as it allows us to progress to
Step 3: Application of the lemma (stronger version), leading to Eehp.
Step 4: What can we do with Eehp ? Let examine the last stage of the 'natural language proof'. This hinges on the triple product
x•ix•x
which is equal to both
(x•ix)•x and x•(ix•x),
hence to
hx•x and x•e.
This is where we might hope to make use of the equality of hx and e. Surely, if hx and e are equal, it is reasonable to infer that hx•x is equal to e•x, equal in turn to x? It's time for another axiom, which we will denote E2:
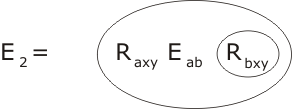
That's pretty self-evident, isn't it? At any rate, putting E2 together with P3 and Eehx we obtain the conclusion Rhxpp :
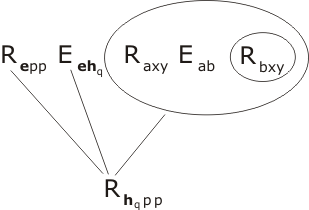
Step 5. We resolve P5, P4 and the result just obtained, Rhxpp, with P1, which means unifying
Rxyu Ryzv Ruzw with Rpiphp Riqqe Rhrss.
We calculate the unifying substitution as follows:
x = p y = ip = iq ∴ q = p z = q = s ∴ s = p u = hp = hr ∴ r = p v = e w = s = p
Therefore
Rxvw = Rpep.
Thus Res(P5, P4, Rhxpp, P1) = Rpep.
Step 6 (if felt necessary). Rpep can be resolved with (Raea) to produce O - and our theorem is proved - albeit with the help of the premises P5, E1 and E2, introduced along the way! ◊
There remains the small problem of showing that ix behaves as a right-inverse, as well as a left-inverse. What we want to derive is Rxixe. But by definition of hx, we have Rxixhx; and at step 3 we derived Eehx. Is that not good enough? Well, not quite: we need another little axiom, another property of Exy, namely:
E3 = (Rabx Exy ( Raby )).
With the help of E3, we are done◊
Postscript: Bring on the computer
Don't miss the postscript (continues on another page...)