P1	(∀x ((Fx ∧ Gx) → Hx)) → (∃y (Fy ∧ ¬Gy))
P2	(∀u (Fu → Gu)) ∨ (∀v (Fv → Hv))
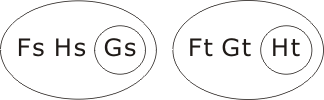
C	(∀s ((Fs ∧ Hs) → Gs)) → (∃t (Ft ∧ Gt ∧ ¬Ht))

Transcription of P₁:

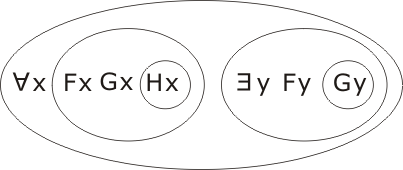
hence

hence

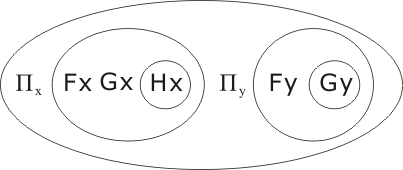
We note that P₁ is not yet actually in clausal form; however, it proves more convenient, on this occasion, to keep it as it is. The transcription of P₂ is:

hence

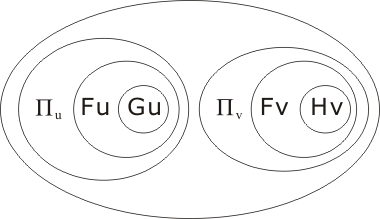
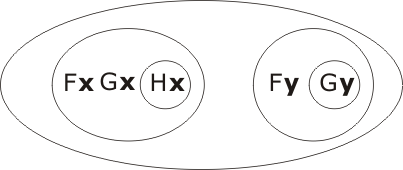
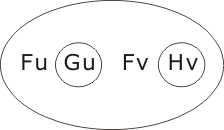
Π_u and Π_v can migrate to the outer space (up two levels), and can then be discarded, leading to

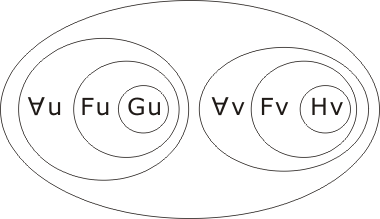
Transcription of ¬C:

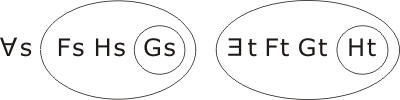
hence

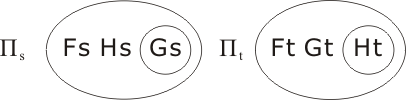
hence

The combined expression P₁∧P₂∧¬C then resolves as:

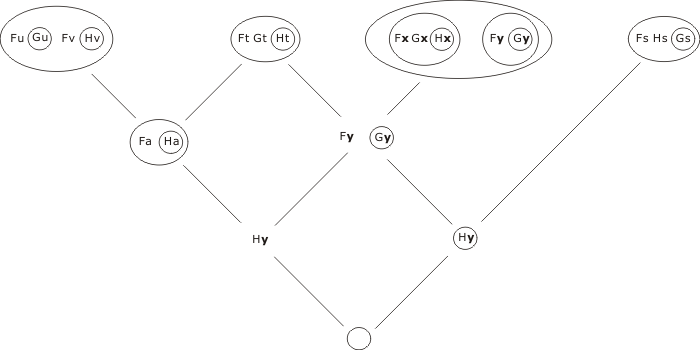
We note that the 'resolution' between the second and third clauses involves first the substitution {x/t}, then an application of the CL-rule

A (A(B)) = AB ≥ B

(where A and B are any CL-expressions), and is therefore perfectly admissible in a proof of the claim that a CLS-expression is mark-equivalent - which is what we are doing here.

---

If desired, the proof can be done 'by the book' - i.e. using clausal resolution. The first thing is to convert the premise P₁ into clausal form, which can be done by using the CL-rule

repeatedly. Thus P₁ is transformed as follows:

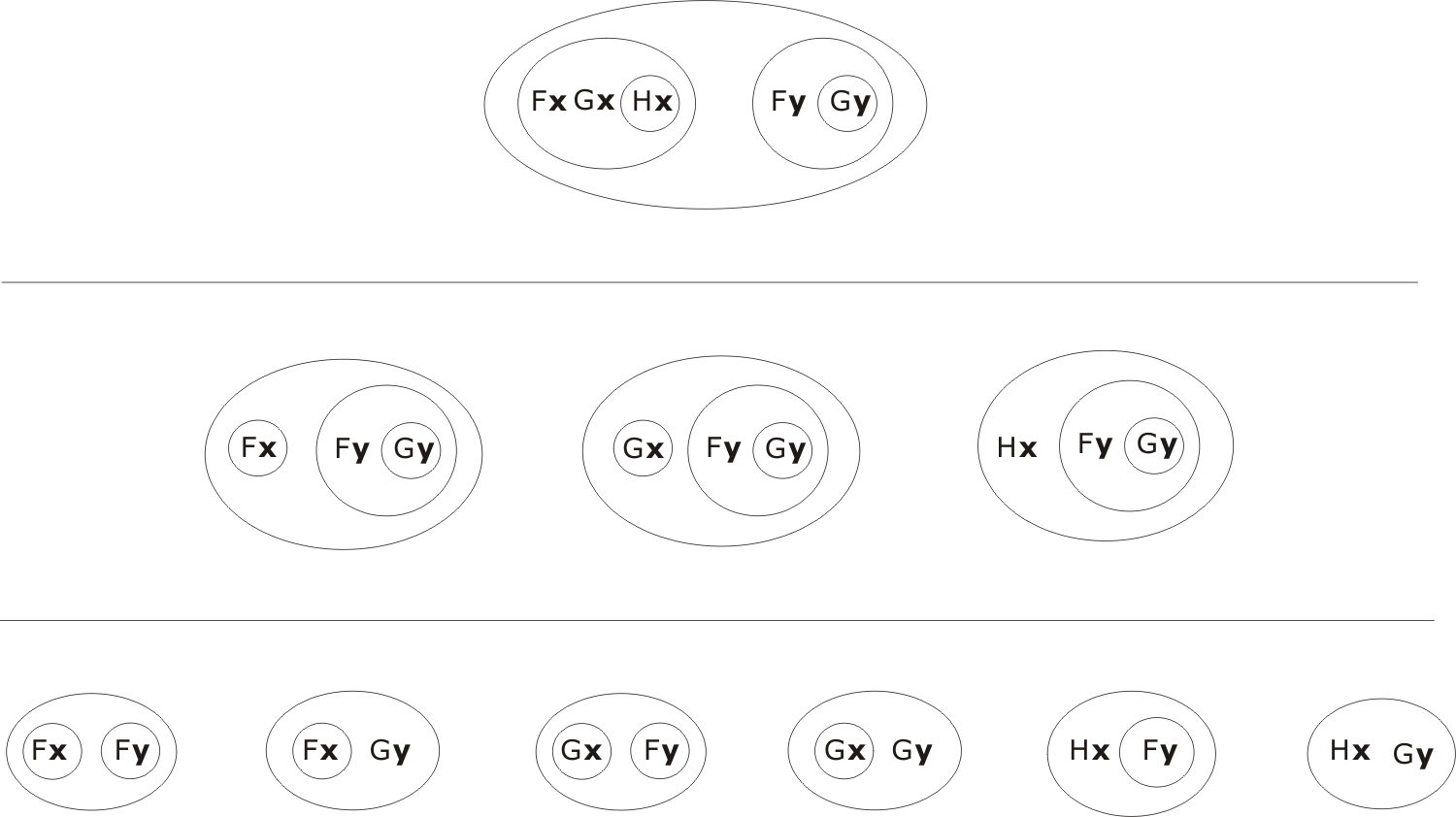
Now combine with

(Ft Gt (Ht))

and 'breed'. It is left as an exercise for the reader to obtain the clauses F_y and (G_y) by this means. (Answer here.)

Solution

We first symbolize the known facts about A, and the statement that is to be proved, by formulae of first order logic.

The existence of • we represent as follows:

P1	∀x ∀y ∃z Qxyz

Here the predication Qxyz means 'z is the result of combining x and y using •'. One way of representing the property of associativity would be to introduce a second two-place predicate meaning 'equals'; but there is another way of doing it. We make the statement:

P2	∀x ∀y ∀z ∀u ∀v ∀w (Qxyu∧Qyzv) → (Qxvw ↔ Quzw)

In words: if u is x•y, and v is y•z, then w is x•v iff w is u•z. The remaining premises are:

P3	∀x ∀y ∃a Qaxy
P4	∀x ∀y ∃b Qxby

The statement to be proved is

C	∃e ∀x Qexx

When we transcribe into Laws of Form notation, P₂ (associativity) may be split into two clauses:

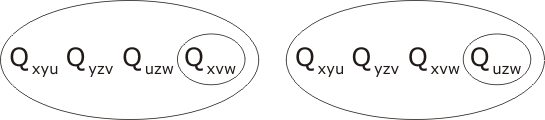
P₁, P₃, P₄ and ¬C become simply

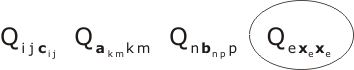
For the proof by resolution, we need only the first clause of P₂, and do not need P₁; we also use P₄ twice. The resolution-scheme is:

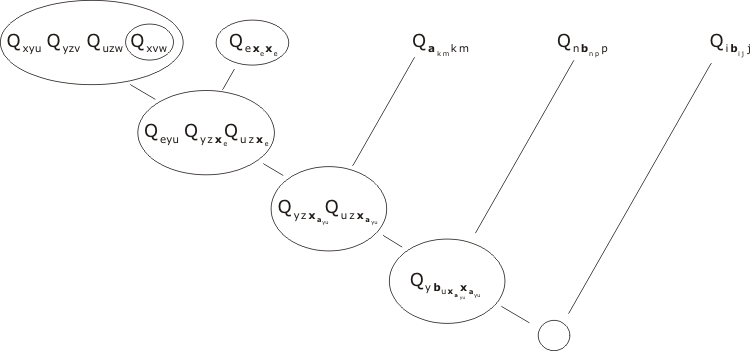
(click on the diagram to bring up a magnified version). This is heavily dependent on unification - perhaps a more detailed explanation is in order? The first resolution step involves unification (one-making) of the terms

Q_xvw, Q_exexe .

This is achieved by the substitution

{ e/x , x_e/v , x_e/w } .

Remember, the substitution acts on the whole of both expressions which are participating in the resolution step, so all occurrences of x, v and w are replaced by the specified terms. The second step involves unification of

Q_eyu, Q_akmkm,

achieved by means of

{ y/k , u/m , a_yu/e }.

This is why the term x_ayu appears in the resolution product. Next, we unite

Q_uzxayu, Q_nbnpp

by means of

{ u/n , x_ayu/p , b_uxayu/z };

and finally we must unite

Q_ybuxayuxayu, Q_ibijj.

Acting on the two terms at first with the substitution { y/i , x_ayu/j }

they become

Q_ybuxayuxayu, Q_ybyxayuxayu.

All that is needed to achieve complete union is to follow up with the substitution

{ y/u }

(or vice versa); then the term in the circle can be uncopied, leaving the sought-for empty mark - our goal! It is interesting that the 'automatic' resolution process finally arrives at the 'insight' that y must be set equal to u - even though it leaves it to the last possible moment. Whereas a typical human approach to the problem of deriving our conclusion C starts with the insight that if there is a left-identity e, then it must coincide with a solution of the equation

e•x = x, ...(1)

where x is some arbitrarily chosen element of A. (The equation must have a solution by premise P₃.) A 'human-style' proof might continue as follows:

Let c be any element of A; then, by P₄, there exists a element b such that

x•b = c . ...(2)

Then e•c = e•(x•b) (by (2))
= (e•x)•b (by P₂)
= x•b (by(1))
= c (by(2)).

But c was any element of A; we may therefore conclude:

∀c e•c = c,

a statement which verifies our original claim C ◊

Let's see how our 'human' proof could be formalized in the language of the CLS-calculus. Let x be a fixed element of A. We first note that

Q_aijij » Q_axxxx

(the left-hand expression reprents the premise P₃). Secondly, flowing from P₄

Q_fbfgg » Q_xbxcc

Next, bringing in the first clause of P₂, and repeating the consequence of P₄ just derived:

Q_axxxx Q_xbxcc Q_xbxdd (Q_xyu Q_yzv Q_uzw (Q_xvw))
» Q_xbxdd (Q_xbxcw (Q_axxcw))
» Q_axxdd

Thus our conclusion is 'implicated' in the premises. The skill lies in revealing that fact; it could be compared with the skill of the sculptor, who reveals the figure that is 'implicated' in the block of marble.

To tackle this, we first need to recall the group axioms. A group is a set G with • and e such that

• • is associative: ∀x,y,z (x•y)•z= x•(y•z)
• every x satisfies e•x = x•e = x
• each x has an inverse y such that x•y = y•x = e

In this problem, the third axiom is redundant, as each element is its own inverse. This leaves us with five premises and a conclusion, as follows (P₁ and P₂ are the two halves of the statement of associativity, as in Example 10.8):

P1	∀x ∀y ∀z ∀u ∀v ∀w (Rxyu∧Ryzv∧Ruzw) → Rxvw
P2	∀x ∀y ∀z ∀u ∀v ∀w (Rxyu∧Ryzv∧Rxvw) → Ruzw
P3	∀x Rxxe
P4	∀x Rexx
P5	∀x Rxex
C	∀a ∀b ∀c Rabc → Rbac
¬C	∃a ∃b ∃c Rabc ∧ ¬Rbac

For the proof by resolution, we proceed in four stages:

Stage 1

We use P₁, P₃ and P₅:

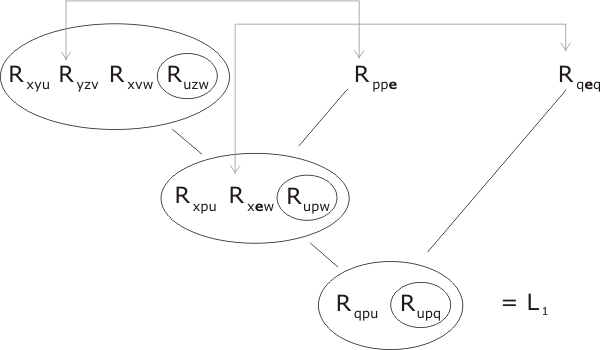
(The grey arrows indicate the terms that are united at each step. L₁ is used as a label for the second resolution product, as is L₂ in the next stage.)

Stage 2

We use P₂, P₃ and P₄:

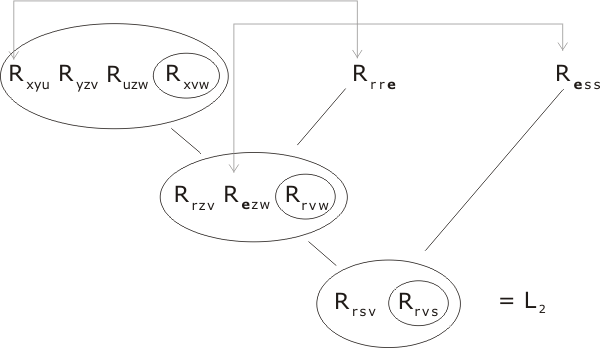
Stage 3

This time we use the first half of ¬C, L₁ (twice), and L₂. Note that when L₁ is applied to a term Rxyz it has the effect of swapping the 1st and 3rd indices; L₂ on the other hand swaps the 2nd and 3rd indices.

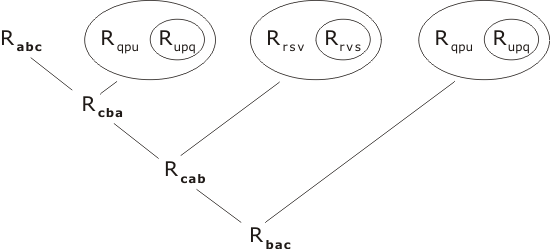
Stage 4

We bring in the second half of ¬C:

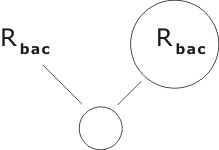
It is left as an exercise for the reader to translate the resolution-proof into a human-friendly form.