CHAPTER TEN
Examples
Example 10.1
For our first example we take the one that came up in Chapter 6, when we first introduced the topic of universally valid implications:
| P1 | ∀x (R(x)→H(x)) |
| P2 | R(t) |
| C | ∃y H(y) |
A possible interpretation is:
P1: All rich people are happy
P2: Tony is rich
C: Somebody is happy
Is it true that P1 and P2 imply C, in all models? The test is to see whether or not the conjunction W = P1∧P2∧¬C is satisfiable. To this end we first of all transcribe P1, P2 and ¬C into Laws of Form notation:
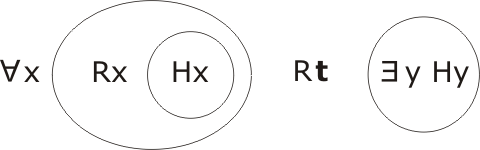
Then re-express ∀x and ∃y in terms of Πx and Πy:
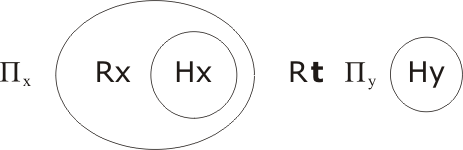
Remove the Pi's (as they are already in the outermost space):
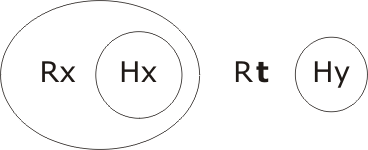
Perform two resolutions, as indicated in the diagram:
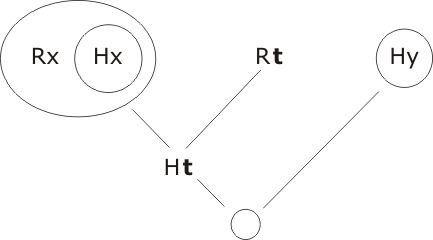
The substitution required for the first resolution is {t/x}; for the second, {t/y}. We have obtained the mark O, therefore W is unsatisfiable and the implication is proved valid. There is no way (no model in which) it couldn't be.
Example 10.2
For our second example we prove the universal validity not of an implication but of a simple statement S. (Actually this may be thought of as an implication but where the premise is simply: nothing - the void.)
| S | ∀x (Px→(∃y Py)) |
We consider the negation of S, transcribed:
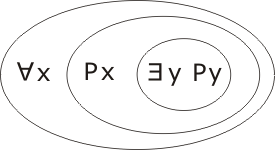
Re-express ∀x and ∃y in terms of Πx and Πy:
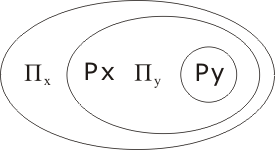
Πx is stuck in level -1, calling for Skolemization: so we remove Πx and replace all occurrences of x by x, leading to
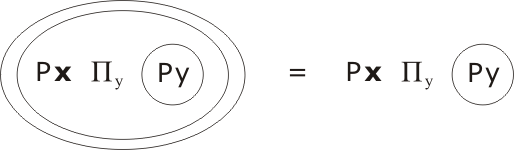
Remove the Πy, and resolve just once this time...
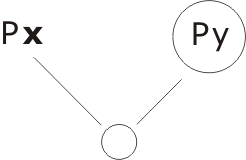
(with substitution {x/y} ). Thus the negation of S is impossible, which means that S itself is universally valid.
Example10.3
A good online source of problems in first order logic is Chapter 8 of the old edition of Symbolic Logic: A First Course by Gary Hardegree. This is Example 3 (page 424):
| P | (∀x Fx) → (∃y Gy) |
| C | ∃x (Fx→Gx) |
The task is to show that P implies C. Here are P and ¬C transcribed:
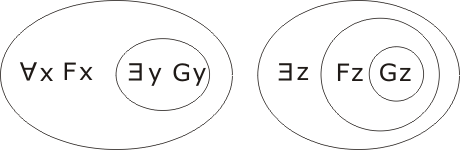
then
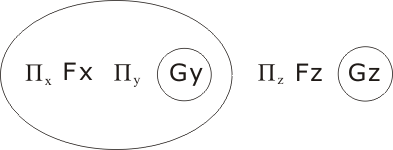
then

with resolution (using substitutions {x/z}, {y/w})
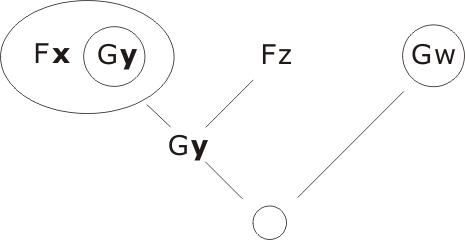
Q.E.D.
Example10.4
This is Example 28 from page 450 of Hardegree:
| P1 | ∀x (Fx → Gx) |
| P2 | ¬∃x(Gx ∧ Hx) |
| C | ∀x (Fx→¬Hx) |
We have to show P1 and P2 imply C. We transcribe P1∧P2∧¬C, changing the 'bound' variables to make them all different:
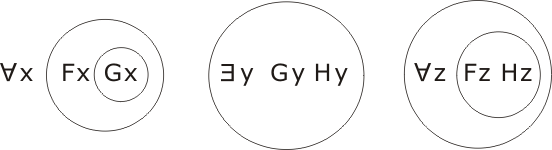
then
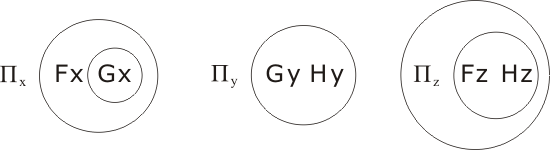
then
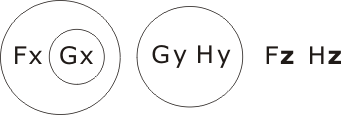
resolving as
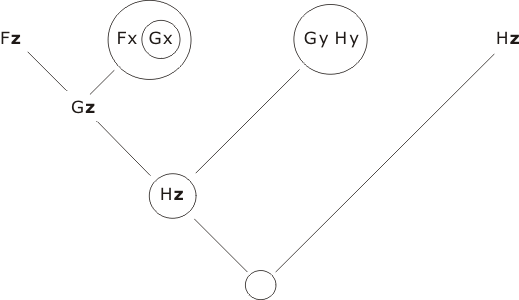
Q.E.D.
Example10.5
This is Example 66 from page 461 of Hardegree:
| P | ∃x (¬∃y (Fy ∧ Rxy)) |
| C | ∀x (Fx→(∃y ¬Ryx)) |
Our task is to show that P implies C. We transcribe P∧¬C, changing the 'bound' variables in C to make them different to the variables of P:
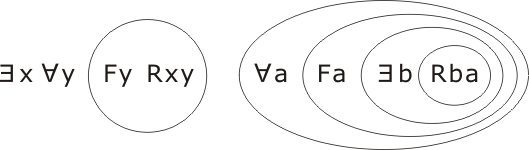
then
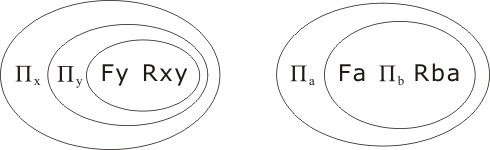
Skolemizing Πx, Πa, then discarding Πy, Πb, we obtain

resolving as
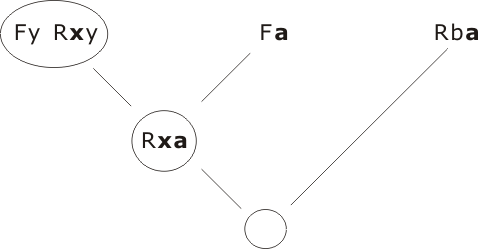
Q.E.D.
Example10.6
This is Example 67 from page 461 of Hardegree:
| P1 | ∀x (Fx → (∃y ¬Kxy)) |
| P2 | ∃x (Gx ∧ (∀y Kxy)) |
| C | ∃x (Gx ∧ ¬Fx)) |
Transcription of P1∧P2∧¬C:
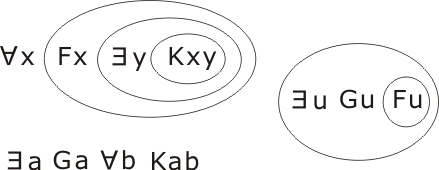
then
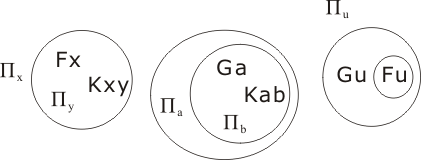
Because Πy lies within the scope of Πx, Skolemization converts y into yx, with subscript x. The variable a, however, is converted into plain a. So we obtain

resolving as
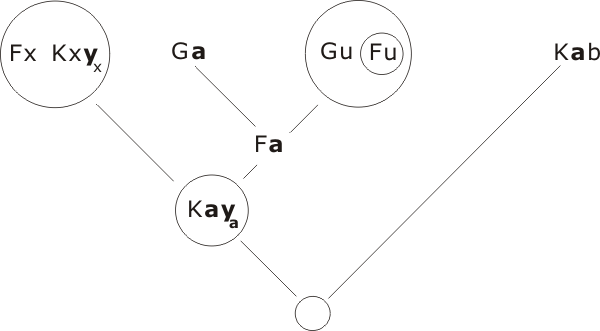
Q.E.D.