Reduction to Standard Form
&
Link Theorem
Note: this page belongs to an older version of this website. It has been superseded by the following pages: The 'Case Analysis' Lemma and Exhaustive Case Analysis and the Standard Form of an Expression.
All the general rules of arithmetic that we know about (so far) have proved to be demonstrable as equivalences in the pure algebra. The burning question, for Algernon, was whether all general rules are similarly demonstrable. The question can be reframed as follows. Let e and f be two algebraic expressions. Each one will contain certain letters. Let A (for alphabet) denote the set whose elements are the letters appearing in e or f, or both. For instance, A might consist of the set {a,b,c,d,y,z}. We say that the equation e=f is valid as a general rule, if e is arithmetically equivalent to f whenever primitive values ( _ or O) are substituted, in e and f, for each letter of A (so that both e and f are transformed into arithmetic expressions). Supposing there are n letters in the alphabet, there are 2n ways of assigning values to the 'variables' (as we may call them) of e and f. Each of these 2n assignments has to be checked, in order to verify a general rule. The equation is valid in the pure algebra, on the other hand, if e can be transformed into f using only legal moves.
Eventually, Algernon's efforts were crowned by success - he was able to answer his burning question. The solution depended on a method of reducing any expression to a standard form: that is what most of the present chapter will be about.
The Depth Lemma
Given any algebraic expression, consider its arithmetic skeleton, that is, what is left when all the letters have been taken out of the expression, leaving a pattern of nested circles. Each space (enclosed by a circle C) in the pattern can be assigned a 'depth' by the following (recursive) rules:
- the depth of a space is one more than the depth of its parent space (i.e. the space outside C)
- if a space has no parent (i.e. if it is the outermost space) its depth is zero
The intrinsic depth of an expression is defined as the depth of the deepest space in its skeleton. (One may sometimes need to refer to the depth at which an expression lies within a larger expression. We distinguish that other meaning of depth by calling it extrinsic depth.) Our first step is to prove the following
Depth Lemma: Any expression is equivalent to an expression whose intrinsic depth is two or less.
Proof: Consider to start with a prime expression of depth three. We show that any such expression can be transformed into a (probably composite) expression of depth two. Here is the skeleton of a typical prime expression of depth three:
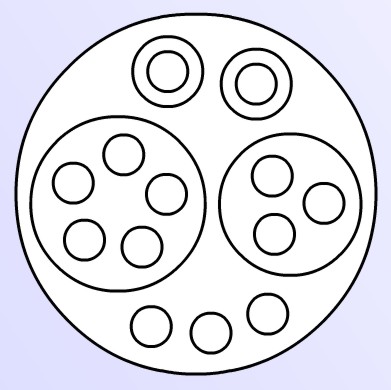
In this example, the content of the outer circle is an expression that is the product of seven prime factors, three of which are empty circles, four of which are non-empty. The non-empty factors contain 1, 1, 3 and 5 empty circles, respectively. In general there could be (say) P empty circles and Q non-empty circles, containing N1, N2, ... NQ empty circles, respectively.
So much for the bare skeleton; to get back to our expression we need to pepper the skeleton with letters. The general prime expression of depth 3 has the form:
e = ( ((a11)(a12)(a13)...b1) ((a21)(a22)(a23)...b2) ... c)
Here c stands for an expression of depth one or less; it includes all the inner factors whose intrinsic depth is only one. Each term aij stands for a collection of letters, placed in a space of depth 3. The index i runs from 1 to Q; then j runs from 1 to Ni. Each bi stands for another collection of letters. We may rewrite the expression as follows:
e = ( ((a11)(a12)(a13)...b1) C1)
with
C1 = ((a21)(a22)(a23)...b2) ((a31)(a32)..b3)... c
Thus all the inner factors apart from the first have been grouped into the expression C1. The depth of the first inner factor may be reduced from 2 to 1, using the depth-reduction move, in its extended form, that can deal with several inner factors at depth 3. We get:
e = (a11 C1) (a12 C1)..(a1N1 C1) ((b1)C1)
The number of factors is N1 + 1. Note that e will still have depth 3, if C1 has depth 2 (as it will do if Q>1). Nevertheless, we have made progress; our next move is to express C1 as
C1 = ((a21)(a22)(a23)...b2) C2
with
C2 = ((a31)(a32)..b3)((a41)(a42)..b4)... c
Substituting this new form for C1 into our last expression for e, each of the N1+1 factors of e becomes a candidate for depth-reduction, reducing the visible depth of the factor to two, at the expense of spreading it out horizontally into N2+1 factors. After this second step of the process, e has been spread out into an expression with (N1+1)(N2+1) factors.
When we have performed Q steps of this type, we find that CQ is after all just c, an expression of depth 1, so that e has finally been converted (by legal moves!) into an expression of depth 2. The number of factors in the shallower expression has grown to
(N1+1)(N2+1)...(NQ+1).
Each of these many, many factors has the form
(x1 x2 x3 ... xQ c)
where each xi is one of the set (with Ni+1 members)
{ ai1, ai2, ai3 ... (bi) }.
This whole process of 'horizontalization' of the expression e could be described (if you liked) as 'multiply-extended depth-reduction'.
Exercise: In the algebra play-area, start with the expression
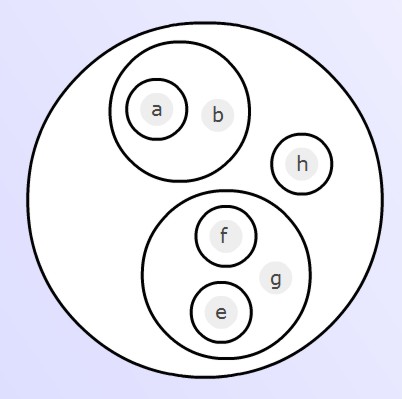
and transform it into
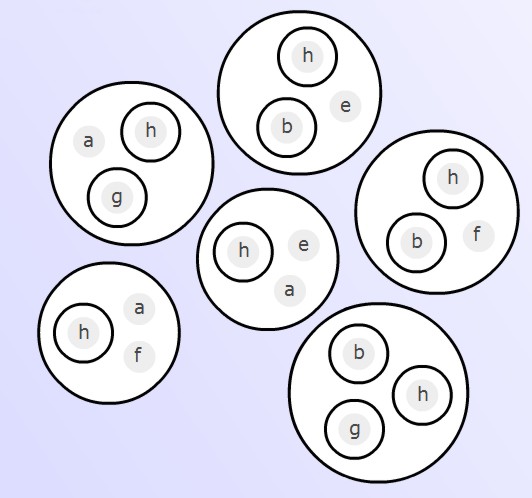
Hint: first rehearse the moves for converting (((a)b)c) into (ac)((b)c) until you have got them off pat. (The moves are given here.)
So far, so good. If you give me a prime expression of depth 3 I can turn it into a (very composite) expression of depth 2. But what if you give me a general expression of depth n (with n≥3)?
If the expression has depth n, that implies that it contains at least one space of depth n. Let all the spaces of depth n be sorted into groups, such that spaces in the same group share the same 'grandparent' (i.e. parent space of the parent space). (Given that n≥3, we can be sure that each deepest space has a grandparent; the depth of the grandparent space will be n-2.) Each grandparent space has a bounding circle. That circle, together with its contents, constitutes a prime expression of intrinsic depth three; which may be transformed into a product of factors, each with intrinsic depth two. We can do the same to each grandparent. Then there will no spaces left at depth n; the intrinsic depth of the whole expression will have been reduced from n to n-1.
Then the whole process may be repeated, until the intrinsic depth of the whole expression is reduced to no more than two. Q.E.D.
The Variable Lemma
So much for the Depth Lemma: we are half way to standardizing our expression. To complete the process we need also the following
Variable Lemma: any expression involving the letter x may be transformed into an expression of the form (x(D)) ((x)(E)) where the expressions D and E do not involve x.
Proof: We may assume (by the Depth Lemma) that the intrinsic depth of the expression has already been reduced to two. Its skeleton will therefore have the form:
(OOO...)(OOO...)(OOO...)...OOO..
The expression itself will have the form
((a11)(a12)....b1) ((a21)(a22)...b2) ..(c1)(c2)..d
where each aij, etc stands for a collection of letters. Apart from d, and the various bi, we may assume that each such collection is non-empty; otherwise the expression may be further reduced in an obvious way. (d may or not be empty.) We may also assume that each collection contains no repeats. (Otherwise, any occurrence of v v, for example, may be replaced by v.)
In each of a11,a12... and b1,b2... and c1,c2... and d, the letter x may or may not appear.
If x occurs in d, all other instances of x may be uncopied, and we are left with an expression of the form xC, where C is an expression not containing x. The expression may then be transformed into an expression of the desired form:
xC = x((C)) = x(x(C)) = ((x))(x(C)) = (x(C)) ((x)(O)) .
Otherwise, if (for some particular i) x appears in bi, the letter x may be uncopied from all the aij (with i fixed, j variable) in which it occurs. Then that factor (the ith factor) will take the form (Fx) where F is an expression not containing x (although F may well have depth 1).
If x does not occur in bi, but does occur in some of the aij, the ith factor takes the form
((cx)(dx)(ex)...G)
where c,d,e,G do not contain x. We can collect up the x's using modified collect, converting the factor into
((c)(d)(e)...G) (G(x))
which is of the form H(G(x)) (with H not involving x).
If x occurs nowhere in bi or aij, the ith factor takes the form H (of depth 2, but not containing x).
Each of the terms (ci) is either of the form (Fx), or else is just H (not containing x).
In sum, the expression e is equivalent to a product of factors of the form (Fx), factors of the form (G(x)), and factors of the form H (not containing x at all).
Now, any product of factors of the form (Fx) may be transformed into an expression of the same form. Thus
(ax)(bx)(cx)... = (( (ax)(bx)(cx)... )) = (x ((a)(b)(c)...) )
which is of the form (Ax), with
A = ((a)(b)(c)...).
Similarly, any product of factors of the form (G(x)) may be transformed into an expression of the form (B(x)); and the product of terms of the form H may be denoted C. Thus
e = (Ax) (B(x)) C
= ( (x(A)) ((x)(B)) ) C [flip]
= ( (x(A)C) ((x)(B)C) ) [distribute]
which is of the form ( (xD) ((x)E) ) with
D = (A)C
E = (B)C
To cover the cases where the expression contains no factors of the form (Fx), just put A=O (so D=C); to cover the cases where the expression contains no factors of the form (G(x)), just put B=O (so E=C). If there are no factors of the form H, then C = _ .
Thus in all cases, e may be transformed into an expression of the form
( (xD) ((x)E) )
with D and E not containing x; and this may be converted, using flip once more, into
(x(D)) ((x)(E)),
which is the required form to prove the lemma.
Note. We have proved that
e = (x(D)) ((x)(E)).
Substituting x = _ into both sides of this equation, we obtain as a consequence
e1 = D,
where e1 is the expression which results from substituting _ for x in the expression e. Similarly, we find that E is equivalent to e2, the expression which results from substituting O for x in e. Thus in practice, to obtain the expressions D and E, there is no need to go through the long series of steps involved in the proof of the lemma. We may write simply
e = (x(e1)) ((x)(e2)).
The Standard Form
Let's have a look at some particular cases. Suppose our expression e involves only one letter, namely x. Then e may be reduced to the form
(x(D)) ((x)(E)),
with D and E not involving x, and therefore not involving any letters at all (since at no point in the proof of the lemmas did we introduce any new letters! See also the note just above.). D and E are therefore arithmetic expressions, which may be reduced to primitive values, i.e. to _ or O. This gives us just four possibilities for e:
- D=_ E=_ e = _
- D=_ E=O e = ((x)) = x
- D=O E=_ e = (x)
- D=O E=O e = (x)((x)) = O
We now know that any expression involving the letter x (and no other letter) can be reduced to one of these four. Moreover, no two of these expressions can be equivalent to one another, because 1) equivalent expressions remain equivalent when primitive values are substituted for their letters and 2) e=(x(D))((x)(E)) is equivalent to D when _ is substituted for x, and to E when O is substituted for x. Thus
e=(x(D))((x)(E)) is equivalent to e'=(x(D'))((x)(E'))
if and only if
D=D' and E=E'.
Next, let us progress to two letters, x and y. Our expression e may be reduced to
e = (x(D))((x)(E))
with D and E involving only the letter y. But then D and E may be reduced to the forms
D = (y(F)) ((y)(G))
E = (y(H)) ((y)(I))
Substituting back into e we obtain
e = (x( (y(F)) ((y)(G)) ) ((x)( (y(H)) ((y)(I)) )
= (xy(F)) (x(y)(G)) ((x)y(H)) ((x)(y)(I)) [distribute]
e has been reduced to a product of four factors. When primitive values are substituted for x and y, just one of the four factors is non-vanishing and therefore determines the value of e. For example, when x=_ and y=O, then e=G, and so on.
When our expression e involves three letters, x, y and z, say, we can reduce e to the form
(xyz(J)) (xy(z)(K)) (x(y)z(L)) (x(y)(z)(M)) ((x)yz(N)) ((x)y(z)(P)) ((x)(y)z(Q)) ((x)(y)(z)(R))
- and so on.
If e involves n letters, it may be converted into an analogous standard form, the product of 2n factors.
Note that when actual primitive values are substituted for the tokens J, K, L, M, N, etc., any factor whose associated primitive value is _ drops out; while if Q, say, is O (Q being the value taken by e when O is substituted for x, O for y and _for z), then (Q) is _ and the factor containing Q becomes simply
((x)(y)z).
In general, we have that e (involving x, y and z) may be converted into a product of prime expressions, picked out of the set
{ (xyz),(xy(z)),(x(y)z),(x(y)(z)),((x)yz),((x)y(z)),((x)(y)z),((x)(y)(z)) }.
Thus the various equivalence classes of expressions are in one-to-one correspondence with the subsets of this set. The number of subsets (given that the set has eight members) is 28=256: this is the number of inequivalent expressions involving x, y and z.
Going back to two variables, we are concerned with the subsets (16 in number) of
{ (xy),(x(y)),((x)y),((x)(y)) }.
The subsets may be labelled by the binary numbers running from 0000 to 1111, where a 1 in the nth place indicates that the nth member of the set is included in the subset. We have
| e0000 = _ | e0001 = ((x)(y)) | e0010 = ((x)y) | e0011 = x |
| e0100 = (x(y)) | e0101 = y | e0110 = (x(y))((x)y) | e0111 = xy |
| e1000 = (xy) | e1001 = (xy)((x)(y)) | e1010 = (y) | e1011 = x(y) |
| e1100 = (x) | e1101 = (x)y | e1110 = (x)(y) | e1111 = O |
(We made liberal use of each way to simplify the expressions.) All expressions involving just two letters x and y reduce to one of these 16 forms.
Link Theorem
We aim to prove the following:
Let e and f be two algebraic expressions. Then e = f is valid as a general rule of the arithmetic of the mark if and only if e = f in the pure algebra.
Proof: When primitive values (_ or O) are substituted for the letters in e, e becomes an arithmetic expression, which reduces to a primitive value. Let us define the value-table of e: it is a record (in tabular or other form) of the values taken by e for each assignment of values to the letters of e. If e involves n letters, the number of different assignments, and hence the number of entries in the value-table, will be 2n.
Sometimes, when comparing different expressions such as e and f, it may be that some letters appear in one expression but not the other. Let A be the set of all the letters that appear in either of the two expressions (or both). Then one may consider the 'extended value-table' of e, which records the values taken by e when values are assigned to all the letters in A, with the understanding that the value assigned to a letter in the set A, but not actually appearing in e, makes no difference at all to the value of e. The same may be done for f. The point is that the value-tables of e and f may then be compared, even though e does not contain exactly the same set of letters as f. (This does not necessarily stand in the way of their equivalence, as the each way move illustrates.)
Within this proof, we shall denote equivalence in the sense 'valid as a general rule' by the ordinary equals sign = ; and pure algebraic equivalence by the sign ≡ . If g is an expression, by gs we mean g reduced to its standard form.
We first prove the 'if' part of the theorem. Suppose e ≡ f. Then there is a chain of legal moves by which e may be transformed into f. Suppose g is turned into h by applying one of the set of initial moves (using the latitude given by the canons of interpretation, embedding and substitution). Then, we claim, the value-table of h is the same as the value-table of g. The question is, can (firstly) any application of
a → ((a))
to a sub-expression a within g make any difference to the value-table of g? The answer is no, because the value of ((a)) is the same as the value of a under any circumstances. The same applies to
O → O a
and to
a(b) → a(ab).
What this boils down to is 1) each of the initial equations of the pure algebra is valid as a general rule of the arithmetic; 2) the canons of interpretation were first established as a valid means of obtaining new general rules out of old ones; then adopted as axiomatic (unproven) for the pure algebra.
Since each single move does nothing to the value-table, neither does the chain of moves connecting f with e. Therefore the value-table of f coincides with that of e, which means that e=f is valid as a general rule.
We now pass to the 'only if' part of the proof. Suppose e = f. Let e be transformed (in the pure algebra) into its standard form es, so
e ≡ es;
similarly,
f ≡ fs.
Then, since legal moves do not affect value-tables (as shown in the first part of this proof), and since e = f,
es = fs.
But the standard form of an expression is essentially the same as its value-table. If es and fs have the same value-table, they are actually identical. Thus e and f are equivalent (algebraically) to one and the same standard form, which gives us a chain of legal moves linking e to f. Therefore
e ≡ f,
and we are done.
We note a powerful corollary of the Link Theorem:
Corollary: If e and f are two expressions such that (in algebra)
ef ≡ _
then
e ≡ _ and f ≡ _ .
Proof: Given ef ≡ _ , then ef = _ is valid as a general rule in arithmetic; which means that whatever values are substituted for the letters occurring in e and f, the value of ef is _ . In the arithmetic, that certainly implies that the value of e is _ and the value of f is _ . Thus e = _ and f = _ (as general rules of arithmetic) which implies (by the Link Theorem) e ≡ _ and f ≡ _ .
back to The 'Case Analysis' Lemma