Development of the Equivalence Expression
We define
[A|B] = (A(B))((A)B) .
There is an equivalent 'flipped' form:
[A|B] = ( (AB) ((A)(B)) ).
The following properties follow easily from the definition:
[A|B] = [B|A]
[A|A] = _
[A|(A)] = O
[A|_] = A
[A|O] = O
([A|B]) = [(A)|B] = [A|(B)]
[(A)|(B)] = [A|B]
[_|_] = [O|O] = _
[_|O] = [O|_] = O
if [A|B]=C then [A|C] = B.
The last of these is a little harder to prove:
[A|C] = [A|[A|B]] = (A([A|B]))((A)[A|B])
= (A [O|B]) ((A) [O|B]) [uncopy]
= (A(B)) ((A)(B)) [property of [|]]
= B [each way].
Now for the most useful property of [A|B]:
Application Theorem:
[A|B] A = [A|B] B
Proof:
[A|B] A = [ |B] A [uncopy]
= B A = B [A| ]
= B [B|A] = [A|B] B.
(Alternatively, refer to the direct proof of Lemma 8 in Proof by Mutual Dominance.)
Thus, in the presence of [A|B], A may be changed into B, and vice versa, at will. Moreover, A may be changed into B even if A is buried within an expression E, just so long as E is 'in the presence of' [A|B]. This is thanks to the fact that [A|B] may then be copied into the space in which A resides, may do its work of transforming A into B, and may then be uncopied again. So
[A|B] (...((AP)Q)R...)V = [A|B] (...(([A|B]AP)Q)R...)V
= [A|B] (...(([A|B]BP)Q)R...)V
= [A|B] (...((BP)Q)R...)V .
One may think of [A|B] as catalysing the conversion of A into B. It must be present, but is not itself transformed by the transformation.
Nesting
Consider the expression
E = [A | [B|C] ].
Certainly, the interchange of B and C makes no difference to E; what is not so obvious is that neither does the interchange of A and B. So
[B | [A|C] ] = E.
One way to see this is to expand the square brackets into circle-letter expressions. Thus
[B|C] = (B(C))((B)C) = ((BC)((B)(C)))
∴ [A[B|C]] = (A( (B(C))((B)C) )) ((A) ((BC)((B)(C))) )
= (AB(C)) (A(B)C) ((A)BC) ((A)(B)(C)) [distribute] ,
a form which is clearly insensitive to any permutation of A, B and C. Let's call this 'triadic symmetry'.
Now let's go up a level and consider
F = [A|[B|[C|D]]] .
Applying triadic symmetry to B, C, D we see that F is insensitive to any permutation of B, C, D. Applying it to A, B, [C|D] we see that
[B|[A|[C|D]]] = F .
Now A, C, D may be permuted at will; then C or D may be got into the outer position, and the other letters permuted at will. So F is insensitive to all permutations of A, B, C and D.
But more is true. Again applying triadic symmetry to A, B and [C|D] we may get [C|D] into the outer position, so
F = [ [C|D] | [A|B] ] .
So the square brackets may be nested in a different way, and it still makes no difference to F.
It's time for a theorem. Let
Q = [a|[b|[c|...[j|k]...]]]
be denoted 'the equivalence expression of the N letters a,b,c... up to k'. Then Q is equivalent to any other expression Q' formed out of the N letters and the N-1 pairs of square brackets, no matter what order the letters are taken in, and no matter how the forms [|] are nested. (We just assume that each compartment of each form [ | ] is occupied either by a letter or by another bracket-form.) Even when N=5 you can see that there will be quite a few permissible nesting schemes - and the situation will only get worse as N gets larger.
Proof: we make use of 'Exhaustive Case Analysis'. To this end we must consider the value of Q when arithmetic values ( _ or O) are substituted for all of its letters. Suppose we start by substituting _ for every letter. Wherever [ | ] occurs in the resulting expression, we may replace it by _ . Eventually, all the brackets will disappear and in no time at all Q will be reduced to _ .
Now suppose that just one of the substitutions changes, so O is substituted for one of the letters rather than _ . At the place in Q where that letter occurs, [_|_] will change into [O|_] = O. Then the change will propagate up to the next level, and then to the level above that, all the way to the top. Therefore Q will change its value from _ to O.
Now suppose that we substitute O instead of _ for a second letter. Again this will change the value of the square bracket expression in which the letter occurs - whether the change is from _ to O or from O to _ . And the same will happen to all the 'higher up' brackets containing that first one, all the way up to the top. So once again Q will change its value - from O to _ .
We may imagine changing the substitutions again and again, always just one letter at a time. Then each change will result in Q changing its value. Therefore, after an odd number of changes, the value of Q will be O; after an even number of changes, it will be _ .
In other words, Q will have the value O if the number of marks O among the letter-substitutions is odd, but the value _ if the number is even.
Let Q' be another equivalence expression, involving the same letters, but with the letters permuted, and with the brackets differently nested. Again, when _ is substituted for all the letters, Q' will take the value _ . Again, when any single substitution is changed, the value of Q' will change. Therefore, Q' and Q will always have the same value, no matter what values are substituted for the letters. Therefore, by the Case Analysis Theorem, Q' and Q are equivalent expressions in the CL-calculus.
Q.E.D.
We use the following form to denote the multiple equivalence expression of the letters a, b, .. up to k:
[a|b|... |k]
When we are working graphically we use the form
It makes no difference if the letters are put into their compartments in a different order; and the expression is equivalent to any nested form such as:
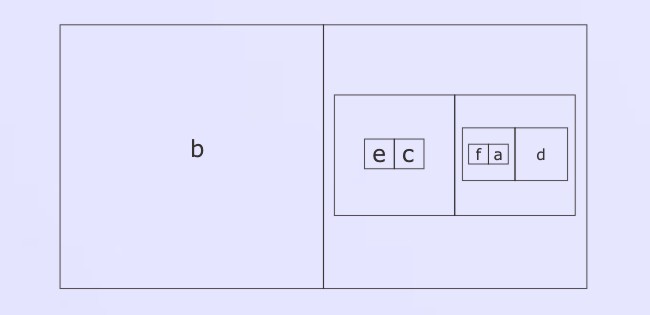
Lemma: in the presence of
Q = [x|a|b|...|f] ,
any occurrence of x, at any depth, may be replaced by [a|b|...|f].
Proof: Q is equivalent to
[x|[a|b|...|f]] ,
so the usual application theorem may be applied.
Example:
[x|a|b|...|f] [x|m|n|...|q] = [x|a|b|...|f] [a|b|...|f|m|n|...|q] .
Another example:
[x|y|a|b|...|f] [x|y|m|n|...|q] = [x|y|a|b|...|f] [y|a|b|...|f|y|m|n|...|q]
= [x|y|a|b|...|f] [a|b|...|f|y|y|m|n|...|q]
= [x|y|a|b|...|f] [a|b|...|f|m|n|...|q] ,
because [y|y] = _ .
For an example of the use of multiple equivalence expressions, see the page on Lewis Carroll's Five Liars Problem.
back to The Mutual Dominance Lemma