How many signs? (Part II)
| n | 0 | 1 | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Number of signs |
1 | 1 | 2 | 4 | 9 | 20 | 48 | 115 | 286 | 719 | 1842 |
| n | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ... |
| Number of signs | 4766 | 12486 | 32973 | 87811 | 235381 | 634847 | 1721159 | 4688676 | 12826228 | 35221832 | ... |
We may illustrate the method of calculation by considering the case n=6. The whole sign may be contained in one circle, or several. In the first case we call the sign 'prime'; otherwise, it is 'composite', and is the 'product' of several primes.
Assuming n=6, if the sign is prime, then it consists of a sign made of 5 circles enclosed in one big circle, giving us 20 possibilities.
In case the sign has two factors, the number of circles in the factors may be 5+1, 4+2 or 3+3. In the first case, the first factor consists of a sign made of 4 circles, enclosed in an outer circle; the second component is just an empty circle; giving us 9 possibilities. The second case gives us 4 possibilities. In the third case, each component consists of a sign made of 2 circles, enclosed in an outer circle. There are 2 signs made of 2 circles, so that looks at first like 4 possibilities. But we don't care which factor is which, so that 4 is reduced to 3. So that's another 16 signs with 2 factors.
If the sign splits into 3 factors, the circles can split up as 4+1+1, 3+2+1, or 2+2+2. The number of signs here is 4+2+1 = 7.
4 factors: 3+1+1+1 (2 signs), 2+2+1+1 (1 sign).
5 factors: 2+1+1+1+1 (1 sign).
6 factors: 1+1+1+1+1+1 (1 sign, consisting of 6 empty circles).
The total number of signs made out of 6 circles is 20+16+7+3+1+1 = 48; agreeing with the number given in the table.
Even with just 6 circles, the 'bare hands' approach to calculating the number of signs is becoming pretty difficult; for higher n, we will definitely need to be more cunning.
As with numbers, but in a more obvious way, each sign may be expressed as a product of 'primes'; for example:
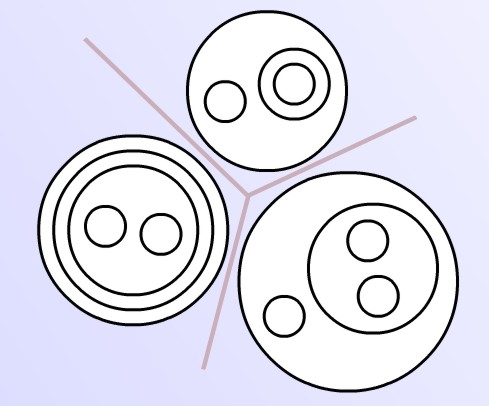
Here the whole sign is a product of three factors, each of which is prime in that it cannot be further divided.
In the case of the natural numbers, we may write (formally)
1 + 2 + 3 + 4 + 5 + 6 + 7 + ...
= (1 + 2 + 4 + 8 + 16 + ...)×(1 + 3 + 9 + 27 + 81 + 243 + ...)×(1 + 5 + 25 + 125 + 625 + ...)×(1 + 7 + ...)×(1 + 11 + ...)×...
With the signs, we may write (formally) something similar:
_ + O + OO + (O) + OOO + O(O) + ((O)) + ...
= ( _ + O + OO + OOO + OOOO + ...)
×( _ + (O) + (O)(O) + (O)(O)(O) + ...)
×( _ + ((O)) + ((O))((O)) + ((O))((O))((O)) + ...)
× ( _ + (OO) + (OO)(OO) + (OO)(OO)(OO) + ...) × etc.
On the left we have a formal sum of all possible signs. On the right, we have one (bracketed) factor per prime sign. Because we are interested in the number of circles per sign, let us 'annotate' each sign in the above formula with a power of x, xn, where n is the number of circles in the sign. The result is
x0 + Ox1 + OOx2 + (O)x2 + OOOx3 + O(O)x3 + ((O))x3 + ...
= (x0+ Ox1 + OOx2 + OOOx3 + OOOOx4 + ...)
× (x0+ (O)x2 + (O)(O)x4 + (O)(O)(O)x6 + ...)
× (x0+ ((O))x3 + ((O))((O))x6 + ((O))((O))((O))x9 + ...)
× (x0+ (OO)x3 + (OO)(OO)x6 + (OO)(OO)(OO)x9 + ...)× etc.
Because the number of circles in a composite sign is the sum of the numbers of circles in the prime factors, the powers of x behave in such a way that the formula remains valid (assuming the powers of x multiply independently of the signs). We now let the signs fade away. On the left, we are left with a formal power series in x, where the coefficient of xn is simply an, the number of signs containing just n circles. On the right, we are left with an infinite product of factors of the form
(1 + xk + x2k + x3k + x4k + ...) = 1/(1 - xk),
one such factor for each prime sign, k being the number of circles in that prime sign. Note that usually there will be many prime signs belonging to the same k. If there are nk of them, the factors will combine to make
(1 - xk)-nk.
But note that nk is just the same as ak-1; so our (valid) equation between power series becomes
1 + a1x + a2x2 + a3x3 + ... = (1 - x)-a0 × (1 - x2)-a1 × (1 - x3)-a2 × (1 - x4)-a3 × etc.
This constitutes a beautiful 'implicit equation' for the coefficients an, first written down by Arthur Cayley (who was analysing a different, but equivalent problem: the number of 'rooted trees' containing n nodes apart from the root)[1]. If all the ai up to i=n are known, then an+1 may be worked out. This works as follows. a0 is known: it is 1. a1 is the coefficient of x in the expression on the right-hand side. a1, a2, a3 etc. are as yet unknown, but that is immaterial, for no factors except the first can contribute to the coefficient of x, which is the coefficient of x in 1/(1-x), namely, 1.
Moving on to a2, the coefficient of x2, no factor on the right-hand side beyond (1 - x2)-a1 can contribute, so again it matters not that a2, a3, etc. are as yet unknown. The coefficient of x2 in
(1 - x)-1 × (1 - x2)-1
= (1 + x + x2 + ...)(1 + x2 + x4 + ...)
is 2, giving us the correct value for a2. And so on... The extraction of the an from Cayley's equation actually requires the consumption of quite a lot of brain power. The equation can be converted into a more convenient form by taking the 'logarithmic derivative' of both sides. Let's call the expression on the left-hand side of the equation, f(x). Taking the logarithm of both sides, we have
ln(f(x)) = -a0ln(1-x) - a1ln(1-x²) - a2ln(1-x³) - ...
Differentiating,
f'(x)/f(x) = a0/(1-x) + 2a0x/(1-x²) + 3a2/(1-x³) + ...
= a0(1 + x + x2 + x3 + x4 + ...)
+ 2a1( x + x3 + x5 + x7 +...)
+ 3a2( x2 + x5 + x8 + x11 +...)
+ 4a3( x3 + x7 + x11 + x15 +...) + ...
= b0 + b1x + b2x² + ... = g(x).
Here bn is the coefficient of xn in the expression on the line before. We have:
b0 = a0
b1 = a0 + 2a1
b2 = a0 + 3a2
b3 = a0 + 2a1 + 4a3
b4 = a0 + 5a4
b5 = a0 + 2a1 + 3a2 + 6a5,
and in general
bn-1 = the sum, over all d dividing n, of dad-1.
Returning to our equation, we may multiply each side by f(x), obtaining
f '(x) = f(x) g(x),
that is,
a1 + 2a2x + 3a3x² + 4a4x³ + ... = (a0 + a1x + a2x2 + a3x3 + ...)(b0 + b1x + b2x2 + b3x3 + ...).
From this (together with the formulae for the bi, see above) we may deduce
b0 = a0 = 1
a1 = a0 b0 = 1
b1 = 3
a2 = (a0b1 + a1b0)/2 = 4/2 = 2
b2 = 13
a3 = (a0b2 + a1b2 +
a2b0)/3 = 12/3 = 4,
and so on. The calculations are best arranged in a tabular form:

The shaded cells are the ones that have to be added up and divided by 6 to obtain a6 (the answer is 48). Then b6 may be worked out, and the calculation continued to the next step.
One might ask, how many of the signs with n circles have the value m (mark) and how many have the value n (not a mark)? The following table gives the answer, for the first few n. cn is the number of signs evaluating to no mark; dn is the number evaluating to the mark.
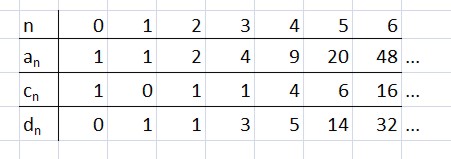
Exercise for the reader: work out a method of calulating these numbers. (Clue: each sign that evaluates to no mark must be the product of primes, each of which evaluates to no mark.)
Exercise: on the whole, it seems that more signs evaluate to m than to n. Calculate (using a computer) the limit, if any, of the ratio dn/cn as n goes to ∞. I make it about 1.8510988385 - but you may be able to improve on this value!
References
[1] Cayley, 'On the Theory of the Analytical Forms called Trees', Phil.Mag 13 (1857) pp. 172-6. (This is available online, in Volume III of Cayley's Collected Mathematical Works. Navigate to page 242.)
See also: Cayley, 'On the Analytical Forms called Trees'